Building acoustic computers with tuneable phononic crystals

For more than two decades, physicists have been investigating wave propagation in phononic crystals, a metamaterial designed to control sound waves. A recent consideration involves using phononic crystals in acoustic computing. Acoustic computers execute basic Boolean algebra computations using acoustic waves. Dirac cones make this possible but achieving them is both very difficult and rare. Professor Sourav Banerjee and his research team at the University of South Carolina, USA, have developed a deaf band-based model for acoustic computing to create and control Dirac cones. This predictive phenomenon creates Dirac-like cones and generates an exclusive opportunity to execute every possible Boolean algebra computation.

Advances in quantum mechanics and condensed matter physics have inspired scientists to explore new ways of manipulating sound based on topological theories. Topological acoustics is a developing field sitting at the intersection of acoustics engineering, mechanical structural design, and condensed matter physics. Considering acoustics’ quantum-like behaviour as topological waves is an emerging development in metamaterials (a class of smart materials that have been engineered to have properties that are not found in nature). For more than twenty years, physicists have been investigating wave propagation in phononic crystals, a metamaterial designed to control sound waves. It is only recently, however, that they have considered using phononic crystals in the construction of acoustic computers.

Acoustic computing

Acoustic computing involves the execution of basic Boolean algebra computations using acoustic waves. Logic gates form the basic building blocks of any digital system. They perform Boolean functions on one or more binary inputs and produce a single output. Four basic gates are the AND gate, the OR gate, the NAND (not and) gate and the NOR (not or) gate. It has been shown that producing basic acoustic logic gates makes computation possible, as it is does with transistors circuits in electronic devices.

Professor Sourav Banerjee from the University of South Carolina, USA, explains that Dirac cones can enable this. Named after the English theoretical physicist Paul Dirac, Dirac cones occur in some electronic band structures (the range of energy levels that electrons can have within a solid) and describe the unusual electron transport properties of materials such as graphene and topological insulators.

Dirac first described electrons as actually spinning and discovered their additional spin degrees of freedom. Phonons are the smallest discrete units of vibrational mechanical energy and referred to as quanta of acoustic waves. Unlike electrons, phonons do not spin, so researchers refer to them as pseudospin states.

Controlling band gaps

Band structures describe the range of energy levels electrons can have, while band gaps describe the ranges of energy that they cannot have. Researchers have been investigating periodic materials for complete acoustic bandgaps for the past two decades and have found many ways to control the width of the bandgaps. Achieving Dirac-like cones, however, is very difficult and rare. Banerjee and his research team have developed a deaf band-based model for acoustic computing to create and control Dirac cones.

We intuitively understand real space where structure is defined in terms of a density function ρ(r) that describes how much matter is at a given point r. In reciprocal space, structure is defined by a function F(Q). This tells us what parts of waves with periodicity Q are required to produce the same arrangement of particles. Reciprocal space enables us to visualise the results of the Fourier transform of a spatial function. A Fourier transform decomposes a waveform into a sum of sine and cosine waves. Reciprocal space is also known as k space, where k is the wavevector, a vector measured in units such as cycle per metre that describes a wave.

Forming Dirac-like cone

Surprisingly, in crystalline materials, the wave dispersion (where wave velocity changes with frequency in a metamaterial) forms a Dirac-like cone at a point known as Gamma point at the centre of the Brillouin zone (polyhedra that contain a single point in reciprocal space).

A flat band is an energy band structure where its energy does not depend on momentum. If a flat band is trapped between two linearly intersecting bands, then no sound can pass through the metamaterial at that frequency. It is as if the band is deaf to that frequency. Due to this acoustical deafness behaviour, this flat band is called the deaf band. The net response of two or more waves is the sum of the individual responses. This is known as superposition. A wave mode can be envisaged as a superposition of two counteractive pseudospin modes. A deaf band is the manifestation of two counterrotating bands effectively cancelling each other out.

The research team have found two ways of forming a Dirac-like cone. The first is to keep a band or a wave mode trapped in between two linearly intersecting bands creating a deaf band. The second is where four bands intersect at the Gamma point. The bands are the wave modes that are possible in a material. A metamaterial could be designed to allow a modal flip, so if two materials have opposite spin states, when they are brought together an acoustic topological insulator is created and a wave propagates along the boundary. The latter is called the quantum spin Hall effect.

Tuning phononic crystals

Acoustic wave control was already possible, and some scientists had created one or two logic gates. Until now, however, no one had been able to create all four of the fundamental logic gates with just one tuneable structure.

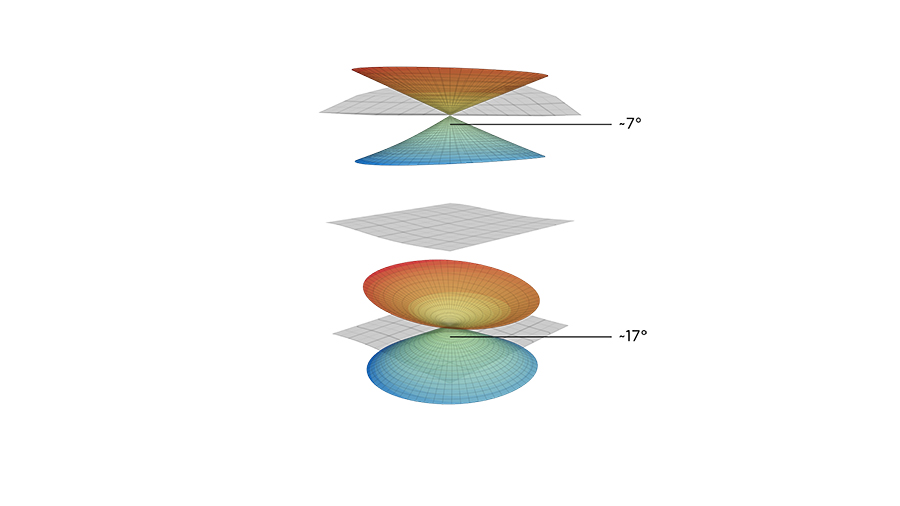
Wave functions are degenerate if they have the same energy levels. They are doubly degenerate if they also have the same symmetry. Double degeneracy states occurring near Dirac-like point in phononic crystals are extremely valuable for acoustic computing. Tuning the phononic crystals results in the bands being separated in one of two ways. Either the bottom band is isolated while the deaf band degenerates with the top band, or the top band is isolated while the deaf band degenerates with the bottom band.

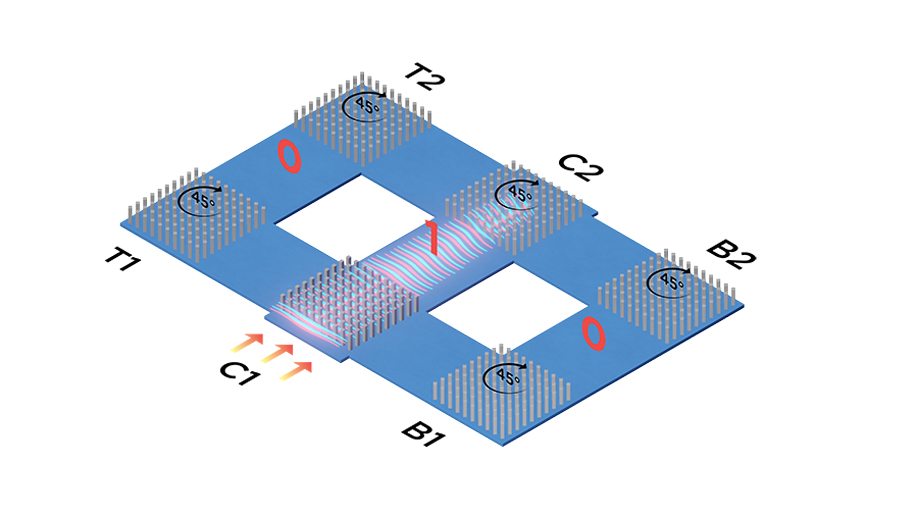
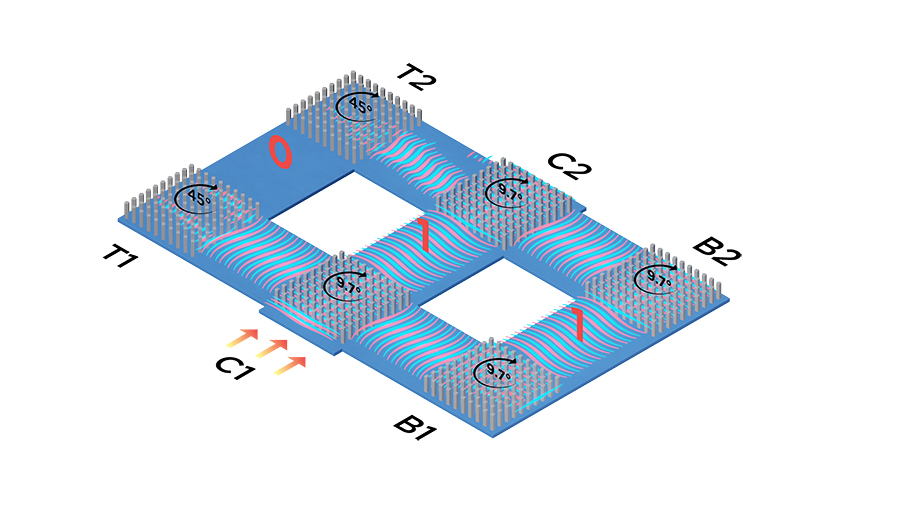
One method to control the width of bandgaps in periodic materials involves tuning square phononic crystals made of polyvinyl chloride (PVC) to widen the bandgaps. The researchers had previously discovered that they could achieve Dirac-like cones by changing the diameter of circular phononic crystals. Unfortunately, they found that the circular arrangement did not suit acoustic computing applications. Instead, they used tuneable square phononic crystals. They found that when they rotate these squares about their central axis, the spatial symmetry is broken, and a Dirac-like cone is created.

Building an acoustic computer

Creating the Dirac-like cone was the gateway to building a simple acoustic computing structure. The researchers arranged a block of 35 X 35 phononic crystal elements in a matrix with tuneable square columns. Two input terminals were added, one on either side of the matrix. The other two directions form the output terminals. The inputs, if not zero, were restricted to the Dirac frequencies, either 12.46 kHz or 18.38 kHz. They discovered that rotating the square phononic crystal through 9.7° creates a Dirac cone. Rotation through 45° results in a bandgap.

The research team ascertained the various combinations of input and rotations required to perform the logic gate AND, OR, NAND, and NOR operations. Extending this concept, they created a six degrees of freedom system to perform more complex computing tasks where all single components are used to perform Boolean algebra (six degrees of freedom refers to the number of axes required for a rigid body to move freely across three-dimensional space). With valid inputs, this predictive phenomenon of acoustic wave guiding creates Dirac-like cones. Unlike previous approaches, it generates an exclusive opportunity to execute every possible Boolean algebra computation.

The exploitation of Dirac-like cones has contributed to the development of orthogonal wave transport, topological insulators, zero index material, acoustic cloaking, wave tunnelling, and the formation of Bessel beams. But above all, it makes acoustic computing achievable. Harnessing the quantum behaviour of acoustics, together with understanding and exploiting the physics of Dirac-cones and Dirac-like cones, has allowed Banerjee and his research team to design a metamaterial that enables the control of the acoustic waves in innovative ways that previously would never have been thought possible and create a new direction of acoustic computing research.