Optimisation of truck-drone parcel delivery using GRASP

Parcel delivery has traditionally been handled by trucks, but rapid technological developments in autonomous unmanned aerial vehicles means that drones are now being used to support parcel delivery. Professor Sarab AlMuhaideb and the research team at King Saud University, Saudi Arabia, have developed an algorithm that minimises the total delivery time for combined truck and drone delivery. The researchers have found a solution to the TSP-D (Traveling Salesman Problem with Drone) problem using GRASP, the greedy randomised adaptive search procedure.

The growth in e-commerce has been accelerated by the coronavirus pandemic, with a dramatic increase in the volume of goods purchased online and delivered directly to the customer. COVID-19 has also strengthened interest in contactless delivery methods, and truck–drone parcel deliveries are already being used in some parts of the world for time-sensitive deliveries, such as medicines, and for deliveries that are challenging for traditional vehicles to complete. Dr Sarab AlMuhaideb, Assistant Professor in Computer Science at King Saud University, Saudi Arabia, and her research team have explored combined truck and drone delivery and developed an algorithm that minimises the total delivery time.

Truck–drone parcel delivery
Parcel delivery has traditionally been handled by trucks, but rapid technological developments in autonomous unmanned aerial vehicles means that drones are now being used to support parcel delivery. Considering the COVID-19 pandemic, drones can also provide contact-free delivery, helping people comply with social distancing rules. The deployment of drones can benefit transportation logistics in several ways, including avoiding traffic congestion, facilitating faster deliveries, and reducing transportation costs. On the other hand, a drone cannot carry heavy parcels, so the parcel weight has an upper limit. Moreover, drones are battery powered, so their delivery ranges are limited, whereas fuel-based trucks can travel longer distances and carry larger, heavier parcels. Even so, traditional truck delivery is slow and comes with high transportation costs.

Combining truck and drone delivery together has the potential to minimise both the total operational costs and the delivery time, thereby enhancing the quality of service. Truck–drone delivery involves drones making deliveries alone, while the truck provides a launch pad for the drone. The delivery driver uses a touchscreen device with a satellite view to direct the drone to the recipient’s address. The drone then releases the parcel and returns to the truck.

Traveling salesman problem
AlMuhaideb explains that this research addresses a variant of the traveling salesman problem (TSP). The TSP is an algorithmic optimisation problem with its roots in operational research and computer science. It is a mathematical problem that aims to minimise cost, so the optimal solution is the cheapest, shortest, or fastest. TSP involves a salesman who has to visit a number of cities. The order in which he visits the sites doesn’t matter provided he visits each one during his trip. He must finish back at the original city where he started his journey. The objective is to find the shortest possible route that allows the salesman to visit each city exactly once before returning to the original city. The problem is often expressed as an undirected weighted graph, a network with nodes representing the cities and arcs indicating the links between them. Each arc has a weight, or cost, associated with it, denoting how difficult it is to traverse this link of the journey, eg, the length of the arc, the time required to traverse it, or the price of a train or airplane ticket. The salesman wants to minimise both the travel costs and the distance he travels.

Considering the COVID-19 pandemic, drones can also provide contact-free delivery helping people comply with social distancing rules.

Traveling salesman problem with drone
The traveling salesman problem with drone (TSP-D) is an extension of the TSP, a vehicle-routing strategy that enables the modelling of drone-based delivery systems. AlMuhaideb describes how TSP-D is a combinatorial optimisation problem where a truck and a drone collaborate to deliver parcels to customers, while minimising the total delivery time. The TSP-D problem is also defined on a graph of nodes and arcs, with the nodes representing the locations, or addresses, of the customers awaiting delivery of their parcels. A customer can be served either by a truck delivery or a drone delivery. In the case of a drone delivery, the algorithm generates three pieces of information, which are required for the delivery route: the node where the truck launches the drone; the node that the drone delivers the parcel to; and the rendezvous node where the truck and drone are reunited.

The objective of the TSP-D is to find the route with the shortest delivery time, where all customer locations are served by either the truck or the drone. While the pickup, delivery, and recharging times of the drone can be disregarded, the following constraints must be considered:
• The use of the drone is restricted to the maximum time that it can fly without needing to be charged.
• The drone’s path must follow the road on the network for safety.
• Both the truck and drone must start from, and return to, the depot.
• A customer can only be served once, with their parcel(s) delivered either by the drone or the truck.
• The drone’s rendezvous node cannot appear on the route before its delivery node.
• The drone cannot serve more than one customer on its journey from a launch node to a delivery node.

TSP-D is NP hard
Determining the optimal solution of a TSP-D problem is an NP-hard problem. NP and P describe groups of mathematical problems known as complexity classes, namely groups of problems whose level of difficulty can be described in a particular way. P denotes the collection of problems that can be solved using an algorithm in ‘polynomial time’ (ie, the time taken to find a solution is a polynomial function that depends on the size of the input), so their solutions can be found efficiently. NP refers to ‘non-deterministic polynomial time’ and represents the suite of problems where a specific solution can be confirmed in polynomial time, but there is no known way to actually solve these problems in polynomial time. This means that there is a limit to the size of the TSP-D problems that can be solved optimally. The research team have therefore selected to use metaheuristics to solve the problem.

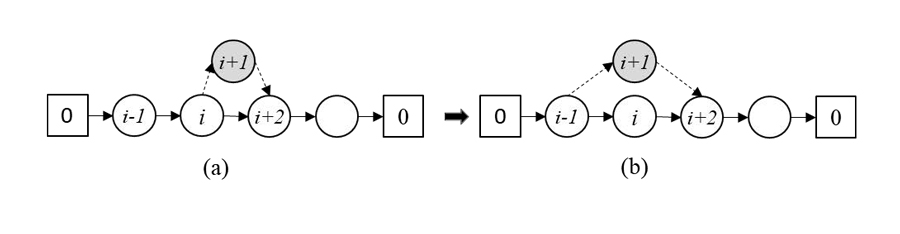
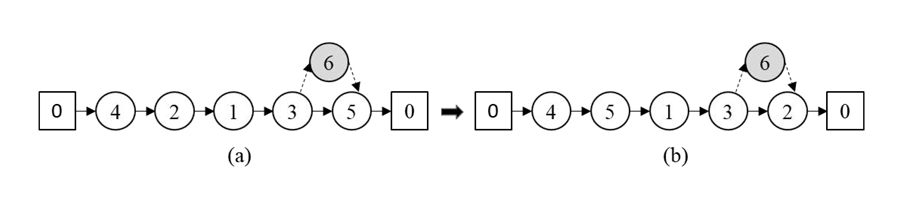
Metaheuristics
AlMuhaideb explains that metaheuristics are adaptive and intelligent algorithms. Their success has already been proven in many similar problems. Metaheuristics are high-level problem-independent algorithmic frameworks that offers strategies for the development of heuristic optimisation algorithms. (A heuristic approach to problem-solving uses practical methods or shortcuts to deliver solutions that may not be optimal but are sufficient for the given timeframe.)

GRASP – a greedy algorithm
In this study, the research team have found a solution to the TSP-D problem using the greedy randomized adaptive search procedure (GRASP). A greedy algorithm is an iterative technique that builds a solution piece by piece through a series of sequential steps. A neighbourhood function is applied to identify potential ‘neighbours’ for each iteration. At each step, it performs a local search and chooses the best solution from those available locally (its neighbours) at that time, without any consideration of future implications for the overall solution.

The objective of the TSP-D is to find the route with the shortest delivery time.

GRASP is a single-solution metaheuristic algorithm. Based on this, the research team have developed an algorithm that starts by constructing the entire truck route as a classical TSP. The route obtained from the TSP is then partitioned into truck nodes and drone nodes, to give an initial TSP-D solution.

The researchers have experimented with a variety of initial routes, or tours, to find out if they could obtain a better solution. They applied several heuristic algorithms that used the local search method to modify the initial tour, and iteratively search for improvements. After considering several neighbourhood functions, two local search alternatives were selected for use in this innovative self-adaptive neighbourhood-selection scheme.

Evaluating the new GRASP algorithm
To test this new approach, the research team used the most challenging scenarios. These had no limits to the drone’s range and both the drone and truck could visit all locations. They applied their approach to 200 examples with different properties, selected from the publicly available ‘Instances of TSP with Drone’ benchmark dataset.

The research team compared the outcomes from their proposed GRASP approach with the results of two studies using state-of-the-art algorithms. The performance of their novel approach compared favourably with that of the two rival algorithms. Non-parametric statistical analysis demonstrated that this new approach has comparable performance, in terms of tour duration, to the rival algorithms (p = 0.074). Moreover, given certain combinations of parameters, such as the drone and truck having the same speed, it outperformed the rival algorithms.

AlMuhaideb concludes that while this study demonstrates the self-adaptive selection of the search neighbourhood for two different neighbourhoods, the method could be easily extended to include more neighbourhoods. She hopes that ‘the self-adaptive selection of the search neighbourhood for the TSP-D problem may also inspire other methods, which in turn may significantly outperform existing ones’.