SAQFT: Algebraic quantum field theory for elementary and composite particles

Quantum field theory (QFT) was a crucial step in our understanding of the fundamental nature of the Universe. In its current form, however, it is poorly suited for describing composite particles, made up of multiple interacting elementary particles. Today, QFT for hadrons has been largely replaced with quantum chromodynamics, but this new framework still leaves many gaps in our understanding, particularly surrounding the nature of strong nuclear force and the origins of dark matter and dark energy. Through a new algebraic formulation of QFT, Dr Abdulaziz Alhaidari at the Saudi Center for Theoretical Physics hopes that these issues could finally be addressed.

The emergence of quantum field theory (QFT) was one of the most important developments in modern physics. By combining the theories of special relativity, quantum mechanics, and the interaction of matter via classical field equations, it provides robust explanations for many fundamental phenomena, including interactions between charged particles via the exchange of photons.

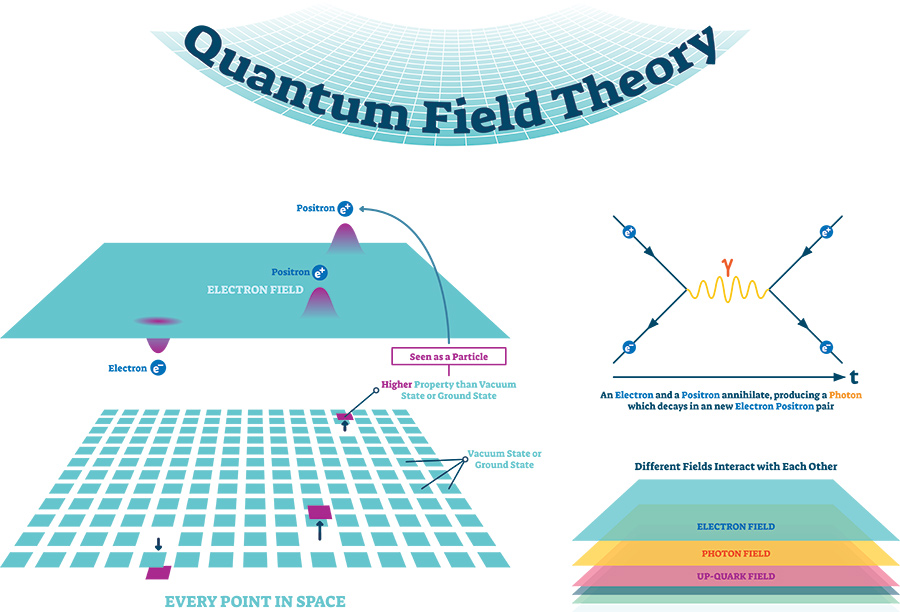
Still, QFT in its current form is far from flawless. Among its limitations is its inability to produce a precise description of composite particles such as hadrons, which are made up of multiple interacting elementary particles that are confined (cannot be observed in isolation). Since these particles possess an internal structure, the nature of these interactions becomes far more difficult to define mathematically, stretching the descriptive abilities of QFT beyond its limits.

Today, QFT has largely been replaced by quantum chromodynamics (QCD), which can describe the binding of elementary quarks to form protons, neutrons, and other composite particles. Yet despite its success, QCD still falls far short of answering some of the most pressing questions in hadron physics.

The drawbacks of QCD

According to QCD, hadrons are made up of two or more elementary particles named ‘quarks’, which cannot exist by themselves but bind together extremely tightly through the strong nuclear force – one of the Universe’s four known fundamental forces. Just as the electromagnetic forces acting between electrically charged particles are mediated by photons, the strong nuclear force is mediated by another family of massless particles, named ‘gluons’.

To explain why quarks cannot exist in isolation, QCD demands that they possess another property named ‘colour charge’, which is continually exchanged by gluons. Yet unlike electrical charges, colour charges can’t be observed directly in experiments – instead, they are a purely theoretical concept, inserted into QCD calculations to maintain consistency in its predictions.

While some physicists are comfortable with incorporating colour charges into fundamental theories, others are concerned that they are only an abstract concept and may not actually exist. If this is correct, it would require physicists to entirely rethink the origins of the strong nuclear force.

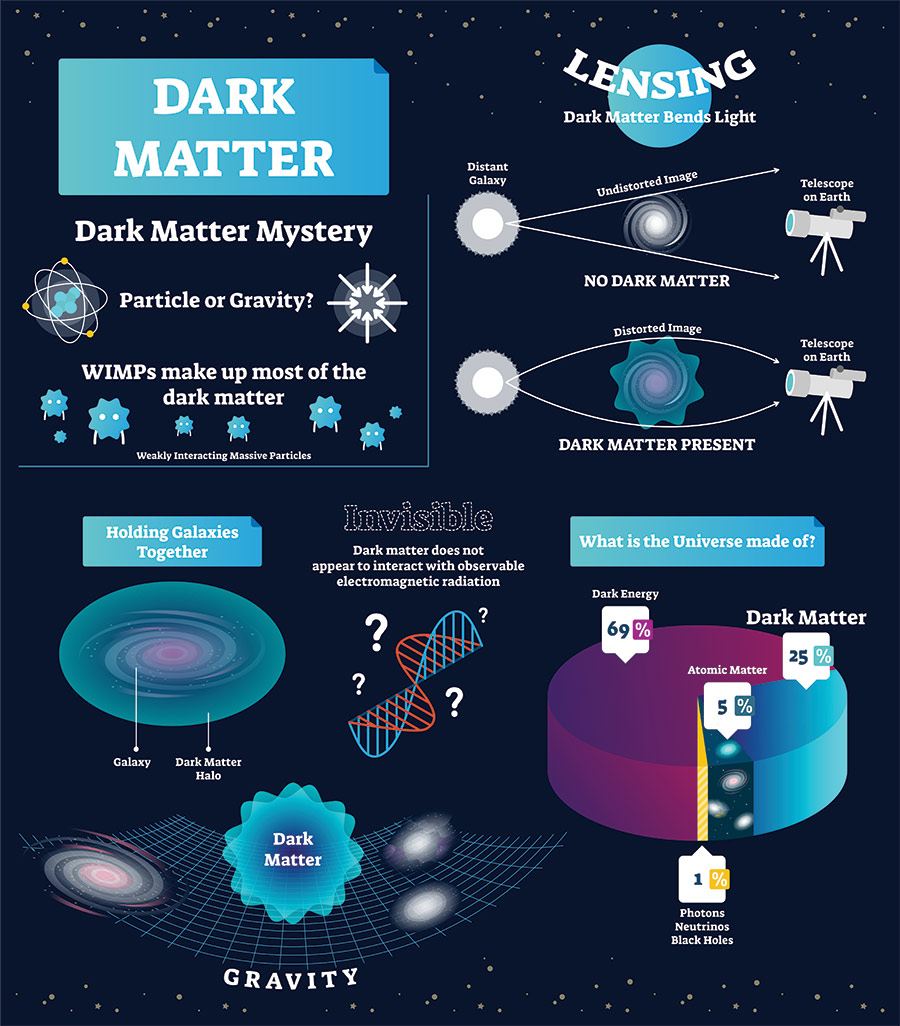
Yet perhaps the greatest concern with the standard model of elementary particle, of which QCD is an indispensable ingredient, is its inability to explain the origins of most of the Universe’s mass, or why the Universe is expanding at an accelerating rate. In the standard model, the emergence of mass is currently attributed to an effect named the Higgs mechanism – but this theory leaves many gaps in our fundamental understanding of the Universe.

According to astronomers’ observations, some 85% of the Universe’s mass is contained in ‘dark matter’, which exerts a gravitational pull but otherwise doesn’t interact with regular matter via the Higgs mechanism.

On top of this, vast amounts of energy seem to be contained in the vacuum of space and are pulling the Universe apart more quickly than gravity can pull it back together. Named ‘dark energy’, this phenomenon also evades any explanation through the Higgs mechanism: a mystery which physicists have now struggled to explain for decades.

Introducing: SAQFT

Dr Abdulaziz Alhaidari at the Saudi Center for Theoretical Physics suggests that the answers to these fundamental questions may have been contained in the QFT framework all along – hidden within the deep mathematical complexity of its explanations for composite particles.

Through his research, he aims to address these main limitations by developing a modified form of QFT. His main goal is to build a framework which can handle elementary particles (with or without structure) more easily, short of any need for more abstract physical concepts such as colour charge.

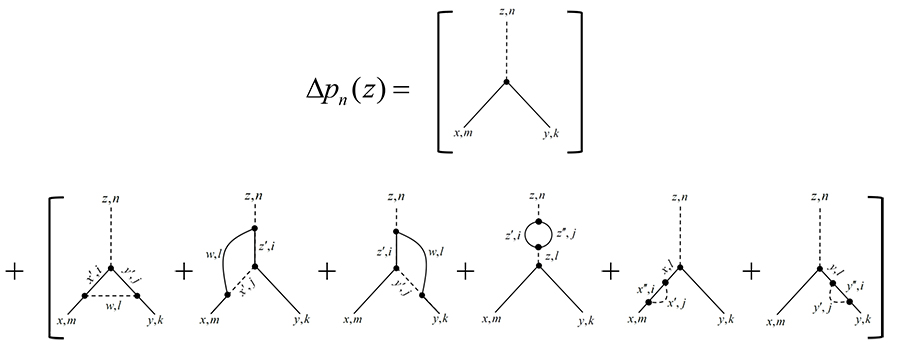
To do this, Alhaidari has developed a new formulation of QFT named ‘Structural Algebraic’ QFT (SAQFT). The models produced by SAQFT can be described using Feynman diagrams: graphical representations of the interactions between elementary particles via force-mediating massless gauge bosons (such as photons or gluons).

To describe these processes accurately, Feynman diagrams often depict closed loops of interactions made up of particles which are required for the interaction to take place, but which don’t appear before or after the interaction has occurred. Instead, they appear at intermediate stages of the process, and disappear before the final products of the interaction emerge.

Essentially, these ‘virtual’ particles are created and annihilated without being detected directly in experiments. Unlike colour charges, however, the nature of these virtual exchanges falls well within the boundaries of conventional physics. By incorporating these loops into its models, SAQFT can replace some of the more abstract consequences of QCD with more well-established physical descriptions, all while maintaining descriptive accuracy.

In addition, as an algebraic theory, SAQFT can be used to show how the variables defining the parameters of quantum fields – used to describe elementary particles – can change from one discrete step in time to the next. This can be done relying on simple algebraic relations pertaining to orthogonal polynomials instead of complex wave equations – significantly simplifying the mathematical descriptions of conventional QFT, making it far easier to model the interactions taking place within composite particles.

Ingredients and postulates

Altogether, Alhaidari’s SAQFT has two main ingredients. The first of these is a specialised sequence of ‘polynomial’ functions, where each function is connected to the two neighbouring functions in a specific way. Secondly, its mathematical operators underly the creation and annihilation of virtual particles within closed Feynman diagram loops that describe how they interact with the energy levels of elementary particles.

Along with these two ingredients, SAQFT is built on five key postulates: firstly, that quantum fields can be represented as superposition of a particle’s quantum energy levels (continuous and discrete); and secondly, that a system’s creation and annihilation operators follow a specific set of rules when acting on each other. Thirdly, the polynomial functions used to build SAQFT must be orthogonal to each other in a certain mathematical sense; and fourthly, basis functions should be combined in such a way that they can approximate any other function. Finally, interaction in SAQFT results from a tensor coupling among the orthogonal polynomials of the interacting quantum fields.

Revisiting fundamental questions

Through his examination of SAQFT’s abilities, Alhaidari has already identified two key areas where the framework could provide better explanations for fundamental processes than QCD. Firstly, it offers an alternative approach to studying the internal structures of hadrons such as protons and neutrons, without resorting to the colour charges demanded by QCD. In turn, SAQFT could help to simplify calculations in nuclear physics.

On top of this, SAQFT offers an alternative approach for explaining why elementary particles possess mass, beyond the Higgs mechanism proposed in the standard model. As a result, Alhaidari hopes his theory could pave the way for new solutions to the origins of most of the Universe’s mass, and the reason why the Universe is expanding at an accelerating rate.

A new alternative to QCD

For now, Alhaidari acknowledges that more work will still be needed to fully develop his theory. Through his current research project, he aims to identify promising areas for future research with an alternative approach to QFT.

To start, he will aim to show how SAQFT can reproduce the most important results of quantum electrodynamics, which describes how light and matter interact with each other.

Building on these results, he then hopes to explore how his framework could be applied to computing processes in nuclear physics and compare the results to the outputs of QCD.

Alhaidari predicts his ideas could cause physicists to reconsider whether the standard model is really the best framework for describing the fundamental nature of the Universe. If his ideas become more widely accepted, he ultimately hopes that SAQFT could form the foundations of new theories, which might help us to finally answer some of the most pervasive questions in physics.