Consciousness and Quantum Mechanics wherein Planck’s constant becomes a variable

The dawn of the 20th century saw physicists embarking on a colossal experimental study of subatomic particles including electrons, protons, and neutrons. As their work progressed, they obtained an abundance of strange results that contradicted the rules of classical physics. Sometimes these extremely small and very light things behaved like pointwise objects, or particles; while at other times they behaved like distributed objects, or waves. Moreover, unlike the classical material objects that could only be in one state at any given moment in time, it appeared that these novel subatomic particles could be in several states simultaneously. This almost ubiquitous property renders subatomic particles more suitable for signifying spiritual objects such as mind and consciousness, than material objects.

Planck’s constant
In 1900, the German physicist Max Planck broke with tradition, making the assumption that electromagnetic waves could only vibrate at specific frequencies. These frequencies are whole number multiples of a wave’s energy, divided by a base constant called ħ (h-bar), which has the value 1.054571817 × 10^-34J.s. This quantum unit, known as Planck’s constant became one of the fundamental constants of physics.

Quantum Mechanics and brain behaviour
By the mid-1920s, physicists overcame these contradictions with a new theory: Quantum Mechanics. This fundamental theory has rules that allow associations previously forbidden by classical physics and now provides the standard formulation for physics.

At this time, the illustrious mathematical biologist Alfred Lotka put forward his quantum model of consciousness where the mind controls the brain with random quantum jumps. Lotka suggested that consciousness takes place “below Planck’s constant”, where the deterministic laws of classical physics are invalid. Today, a number of neuroscientists are researching how quantum theory could provide the solution to fully understanding how the brain works.

In his recent book, Generalized Lagrangian Approach and Behavior of Living Systems, Professor Uziel Sandler, Bioinformatics Department Chair at Lev Academic Centre (JCT), explains that prior to his research, Quantum Mechanics could not be used to explain brain behaviour. To observe quantum effects, the quantum uncertainty of the energy must be greater than the energy of the thermal fluctuations. Thermal fluctuations, however, are proportional to temperature and unfortunately neurons are too hot and too slow to observe quantum effects. Furthermore, the quantum uncertainty of the energy is proportional to Planck’s constant, yet Planck’s constant is too small for this to occur, so the thermal fluctuations effectively erode any quantum effects.

Quantum Mechanics has rules that allow associations previously forbidden by classical physics and now provides the standard formulation for physics.

In 1933, Paul Dirac put forward a conjecture that the amplitude of the probability of transition of a quantum system from its initial state to its final state is proportional to an imaginary exponent of classical (Hamiltonian) action. This turned out to be a flash of genius. Later in 1948, Richard Feynman presented his landmark paper containing a formulation of quantum mechanics based on Dirac’s principle.

Lagrangian dynamics
While Lagrangian dynamics with Hamiltonian Action can be applied to non-living physical systems, it cannot be applied to living systems. Lagrangian/Hamiltonian dynamics result in time-reversible equations of motion and to energy conservation, which does not hold for living things.

The new generalised Lagrangian
In his book, Professor Sandler demonstrates how expressing the causality principle in fuzzy logic form together with features of the local topology of a system’s state space unexpectedly led him to the Lagrangian/Hamiltonian equations of motion with a natural extension of the Lagrangian and the Hamiltonian Action. This finding facilitates the description of the behaviour of living systems by applying the powerful apparatus of Lagrangian dynamics to a broad class of behaviours ranging from simple chemotaxis to the relationship between homeostasis and drug addiction, and to the behaviour of human populations in an environment.

The generalised Lagrangian can depend on both the action and its conjugate variable w. Employing the Dirac-Feynman approach with the generalised Lagrangian and Hamiltonian Action leads to a corresponding extension of Quantum theory, where both the wave function and Feynman propagator depend on this conjugated variable; whereas this variable becomes equal to the reversed Planck’s constant w=1/ħ for quantum mechanics with common (i.e. action independent) Lagrangians. The novel Quantum concept is therefore Quantum Mechanics, in which Planck’s constant should be replaced by the Planck’s variable – w. This leads to the appearance of additional terms in the Schrödinger equation and unusual features of such quantum objects.

Unusual properties are revealed
Observability of quantum effects depended on Planck’s constant divided by the mass of the object of interest. If this quotient is very small, which happens when the mass is large, the quantum effects can be neglected, and the objects will demonstrate classical behaviour. In Quantum Mechanics, where the reversed Planck’s variable is replaced by Planck’s variable, the above-mentioned relation can have a large value even when the object is massive. Therefore, even massive objects could demonstrates quantum behaviour. Moreover, this value varies at different times so these objects can demonstrate both quantum and classical behaviour at various time intervals.

At least until now, we do not know of a physical system that could demonstrate sometimes quantum and sometimes classical behaviour, so it is uncertain whether this modified Quantum Mechanics could describe a physical system. On the other hand, it describes exactly what happens in the mind, where consciousness is sometimes uncertain regarding the correct decision and alters between different states, while at other times it deterministically leads to a unique solution. Moreover, since Planck’s variable can be sufficiently small, the quantum uncertainty of the energy could be large enough that the thermal fluctuations will not ‘erode’ the quantum effects.

The stress paradigm
By considering the brain as a collection of interacting neurons, where each neuron is described by a few relevant parameters, we could design a corresponding generalised Lagrangian based on the stress paradigm:
• The main goal of any living being is to avoid destruction or death.
• A basic parameter that indicates the likelihood of death is the level of stress being experienced.
• The natural behaviour of living organisms is to reduce stress.
• The rate of change of stress is the living system’s Lagrangian.

Potential parameters could include the membrane potential and the threshold of the action potential. The brain state (i.e., a group of neurons firing at the same time) can now be assessed as a set of these parameters at a given time.

A key assumption of this approach is that a deviation of the neurons’ parameters from their ground states increases stress, while the neurons’ activity (a time derivative of these parameters) decreases stress.

The common physical Lagrangian depends on position coordinates. In this extended model, the generalised Lagrangian’s “coordinates” and “velocities” are the neuron’s parameters (not to be confused with their positions) and their time derivatives, while the level of stress plays the role of the Hamiltonian Action. This means that the generalised Lagrangian should depend on the stress level and its conjugated Planck’s variable.

For living beings, a key assumption of this approach is that attempting to reduce the likelihood of death by reducing stress governs their behaviour.

Interestingly, the lowest approximation of interconnection between neurons (which in physics corresponds to the so-called “Harmonic” approximation), corresponds to the so-called “Hebb’s interaction”, which is generally accepted throughout neuron network research.

Modelling consciousness
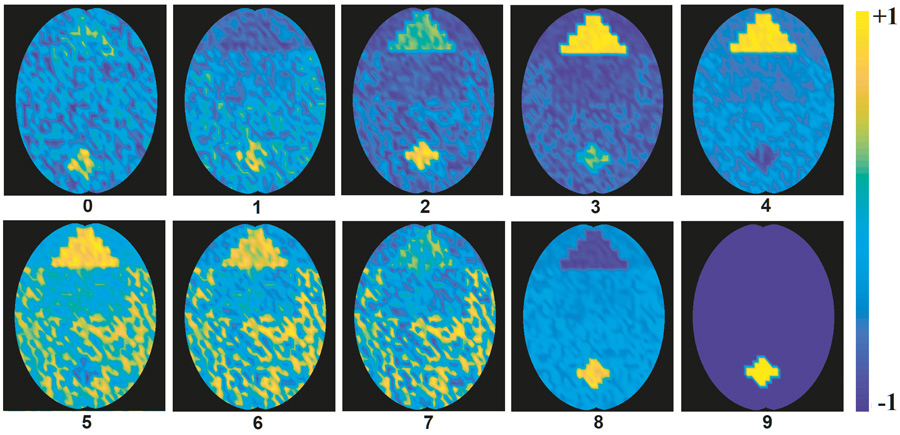
This modified Quantum Mechanics describes consciousness in terms of the behaviour of a wave function and the associated Feynman propagator. This defines the changing expected values of the neurons’ parameters over time. The abovementioned book includes the results from a computer simulation of the expected values of the neurons’ parameters. [See Figure 1] These show that the initial value of Planck’s variable was small, while the initial stress was relatively large. A small Planck’s variable means that the quantum-mechanical probabilistic behaviour of consciousness is likely, and the system fluctuates between various states. This can be interpreted as free will. When Planck’s variable is increased, the behaviour becomes more certain and is less affected by ‘noise’, so the behaviour of consciousness tends towards classical behaviour and in the end the system commits to a single decision. Conversely, if the initial Planck’s variable has a large value, consciousness will demonstrate deterministic classical behaviour at the outset.

When there is enormous initial stress, what the author refers to as “malignant stress”, Planck’s variable could decrease over the course of time and consciousness would therefore remain unstable throughout. This could explain the ‘mindless’ behaviour observed in highly stressed humans and animals.

Wider impact
In his book, Professor Sandler presents a number of applications of the new approach using generalised Lagrangian dynamics to describe the behaviour of living beings and their environment. These are underpinned with the primary incentive driving the social behaviour of living things – their attempt to cope with stress, which forms the biological foundation for this research and empowers Quantum Mechanics to describe living systems and social behaviour.