Keplerian nest of polyhedral structures in different symmetry groups

To a geometer, a polyhedron (plural polyhedra) is a three-dimensional shape with flat polygonal faces. The faces meet at line segments called edges, and the edges meet at points called vertices. The word is derived from the Greek ‘poly’ (many) and the Indo-European ‘hedron’ (face). Often highly symmetric, polyhedra have great aesthetic appeal, and they are common in chemistry, biology, mathematics and other disciplines.

Di Sun, Professor at Shandong University, Stan Schein, Professor at the California NanoSystems Institute of UCLA, and their collaborators are particularly interested in nested polyhedra. Their recent investigation unites two research streams. First, they synthesized and characterized a nest (Ag₉₀) with three polyhedral shells in different symmetry groups. Second, they connected this problem with one solved by the late mathematician John Conway, who used the Zometool to address a similar problem that had been implied by Kepler’s model of our solar system.

The backstory
This study begins with Peter Jon Pearce, an American product designer, author, and inventor. In 1966, he spent a year working with Buckminster Fuller, the renowned inventor and visionary, on illustrations for Fuller’s book, Synergetics (1975). Pearce’s own work focused on high-performance sustainable design, as he later demonstrated in his design of the famous Biosphere 2, an American Earth system science research facility.

Unfortunately, Conway neither said nor wrote anything about the special symmetry properties of his model.

The recipient of a research grant from the Graham Foundation in Chicago in 1965, Pearce began studying spatial geometry, crystallography, and morphology in earnest. This investigation resulted in the publication of his book, Structure in Nature is a Strategy for Design, (1978). In this text, among other innovations, he provided the first description of all of the achiral, convex uniform honeycombs composed of tetrahedral and octahedral polyhedra.

The Universal Node system
In his book, Peter Jon Pearce referred to a modelling system he had created as the Universal Node system. He had designed the system as a comprehensive tool that enabled the physical modelling of any periodic structure rooted in the 7 crystal systems (triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic) and the 14 Bravais lattices (3-dimensional configurations into which atoms can be arranged in crystals). The Universal Node system was essentially based on a system of cubic and octahedral symmetry. 

In 1966 it was not possible to injection mold the node with sockets, so the Universal Node was developed with 26 spokes that correspond to the 13 symmetry axes of the cubic/octahedral system. The spokes were shaped according to the symmetry axes of this system. The 2-fold axes, where a shape appears identical after rotating 180^o, had 12 rectangular spokes. The 3-fold axes, where a shape was repeated after rotating 120^o, had 8 triangular spokes. The 4-fold axes, where a shape was repeated after rotating 90^o, had 6 square spokes. Three different types of branch matched the spokes of their respective symmetry axes. This shape coding ensured that the Universal Nodes always remained parallel during the assembly of networks. These structures of the spokes and nodes built a symmetry intelligence into the modelling system so that these symmetry principles could be experienced by the user. 

In the early 1970s Pearce produced this system as a building toy called SuperStructures, a set with sticks (spokes) and balls (nodes). His system made it easy to create ‘octahedral’ structures, including octahedral Platonic solids, such as cubes and octahedra, and Archimedean solids, such as truncated octahedra, as well as larger free-style structures.

Zometool
A friend of Pearce’s, the inventor Steve Baer, was fascinated with dome geometry and polyhedra. He had been introduced to a toy version of MERO’s cube-based space-frame system in Germany in the early 1960s. He wondered if there was a similar underlying icosahedron-based system, leading to his discovery of the 31-zone system, which showed Pearce’s cubic/octahedral system was one of five related to one another by icosahedral symmetry. Baer’s associate and Drop City cofounder Clark Richert added another 30 zones and completed the icosahedral relationship with Pearce’s 13-zone system. Baer licensed Marc Pelletier and Paul Hildebrandt to develop their design for the user-friendly version of his “Zometoy”. The result, informed by both Pearce’s and Baer’s theoretical and practical experiences, and enhanced by Pelletier’s superlative math, was the Zometool. (The Zometool is recognized by quantum mathematician Micho Durdevich — known for coining the term “quantum computing” — as a physical embodiment of quantum math).

John H. Conway
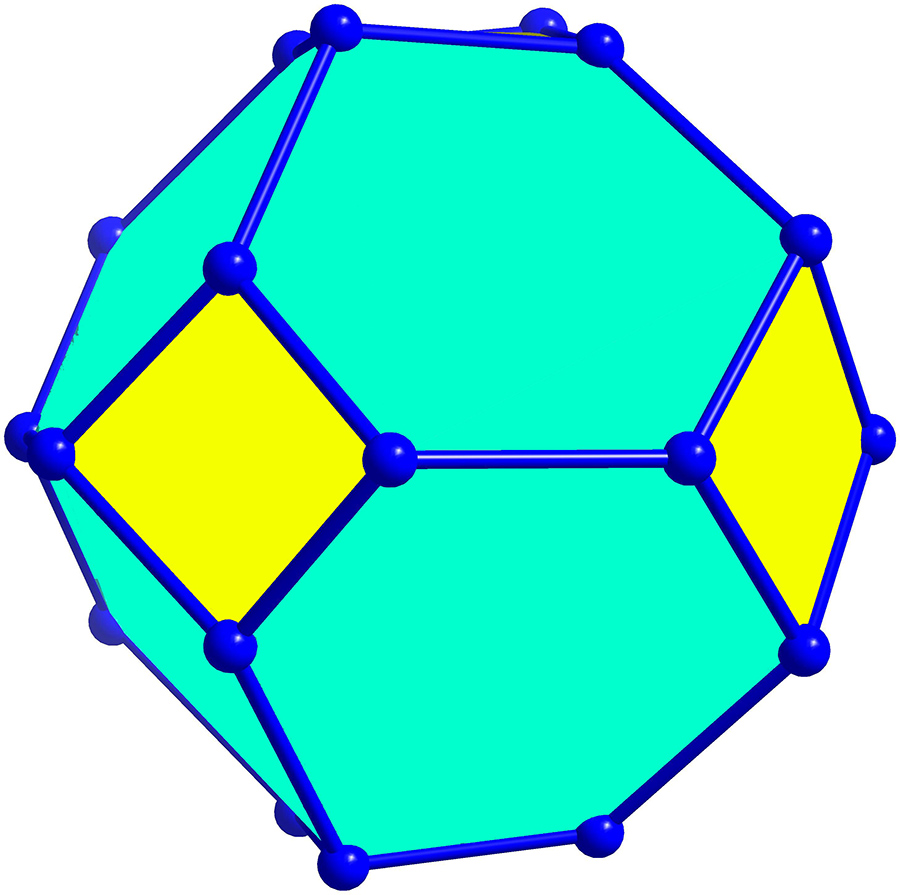
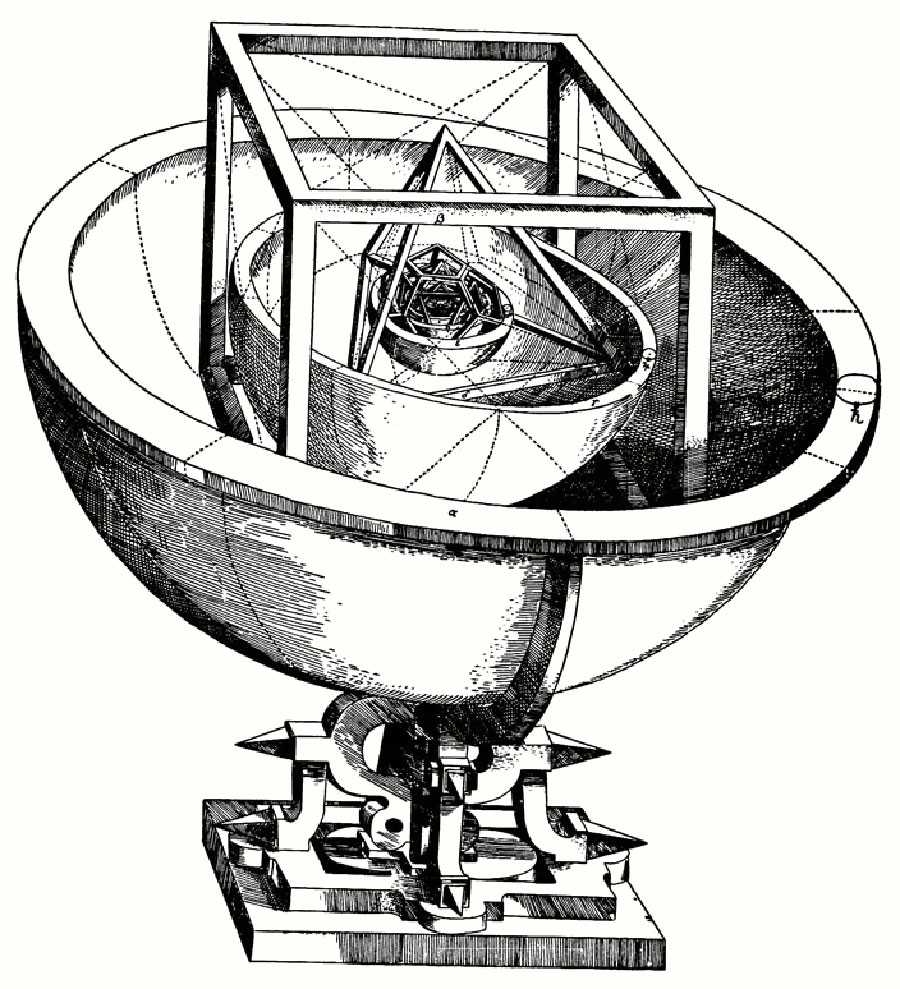
John Conway, an English mathematician, was famous for his love of toys and was one of Zometool, Inc.’s first customers, ordering four Researcher Kits for the Geometry Center at the University of Minnesota. Realising that the Zometool embodied countless relationships among the Platonic Solids, Conway created a model of all five of the Platonic solids with the smallest number of nodes and struts, a model that later became known as ‘Kepler’s Obsession’ or ‘Kepler’s Kosmos’ (Figure 1). This model is still being sold by Zometool. Conway’s model ‘solved’ a four-hundred-year-old problem implied by Johannes Kepler’s model of the solar system.

Kepler’s mystery of the cosmos
In 1597, the German astronomer and mathematician Johannes Kepler published Mysterium Cosmographicum (The Cosmographic Mystery) laying out his philosophy of the universe with its then-known six planets. Kepler believed that the orbits of the six planets could fit around the five “perfect” solids: the octahedron, icosahedron, dodecahedron, tetrahedron and cube.
Kepler’s system proposed that the orbit of Saturn circumscribed a cube. Inscribed in the cube was the orbit of Jupiter that also circumscribed a tetrahedron. Inscribed in the tetrahedron was the orbit of Mars that also circumscribed a dodecahedron. Inscribed in the dodecahedron was the orbit of Earth that circumscribed an icosahedron. Inscribed in the icosahedron was the orbit of Venus that circumscribed an octahedron. Finally, the orbit of Mercury was inscribed in the octahedron. It was an intricate concept that almost worked. Kepler, however, made no effort to align the five solids (Figure 6).

Conway, renowned for his work in symmetry, created a particular alignment of the five solids – the tetrahedral tetrahedron, the octahedral cube and octahedron, and the icosahedral dodecahedron and icosahedron – the challenge being that the solids were in three different symmetry groups. Unfortunately, Conway neither said nor wrote anything about the special symmetry properties of his model.

Kepler’s Kosmos and coordination chemistry
In the second stream of this study, Professor Sun and Professor Schein took the concepts of Conway and Kepler and applied them to coordination chemistry. Coordination chemistry involves compounds with a central cation (positively charged ion) coordinated by an array of molecules or anions (negatively charged ions), the latter called ligands. Many compounds containing metals such as silver and gold centre coordination complexes. The geometrical arrangement varies according to the number and type of ligands bonded to the metal centre as well as the coordination preference of the central atom.

Silver nanoclusters
The investigators explained how, among families of metal clusters, silver nanoclusters benefit from the exceptional versatility of silver(I) atoms. These have flexible coordination preferences, a susceptibility to reduction (gaining electrons), and a tendency to form argentophilic (silver atom to silver atom) interactions with specific structural characteristics and a variety of novel physical properties. These properties enrich the number of members and types of this family.

Silver polygons can form with the help of surface ligands, inner anion templates and argentophilic interactions, enabling the construction of polyhedral structures. Coordination-driven self-assembly has facilitated the creation of molecules mimicking Platonic, Archimedean and even Goldberg polyhedra. More challenging, however, is the assembly of nested polyhedra, both in terms of their synthesis and in determining the alignment of the polyhedra.

The Ag₉₀ nanocluster possesses the most symmetric alignment of 2- and 3-fold rotational axes.

Nested polyhedra
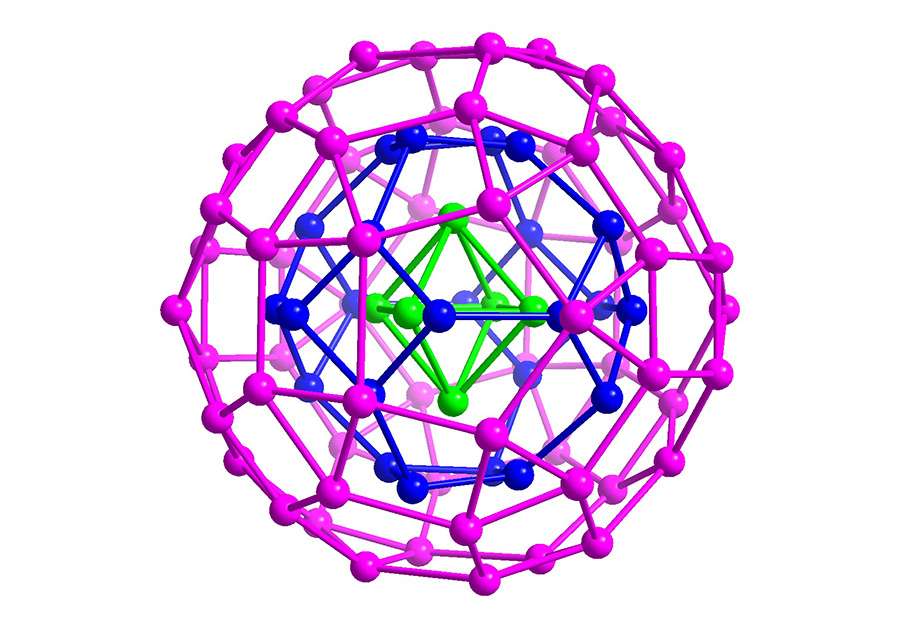
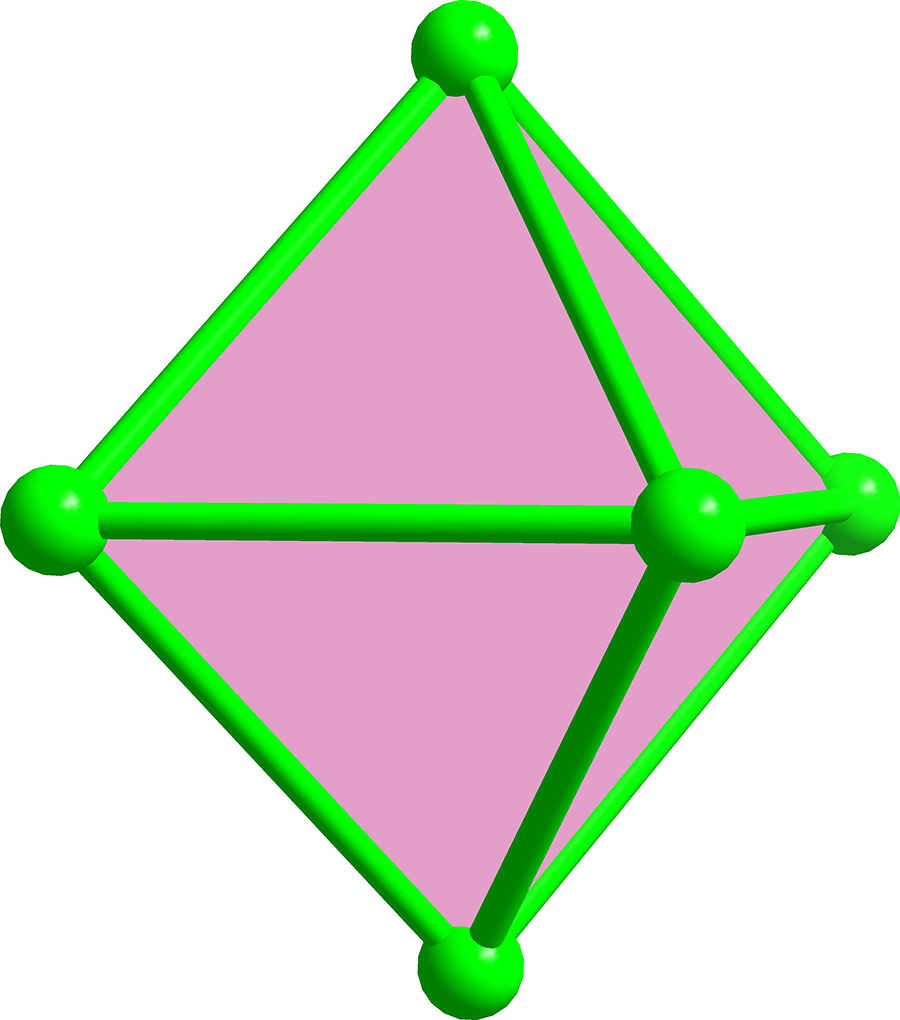
The research team carried out synthesis and X-ray crystallography to determine atomically precise molecular structure of a nest with 90 silver atoms. The nest had three concentric silver polyhedra with apparently incompatible symmetry (Figure 2a): The innermost shell is an octahedron with 6 vertices (Ag₆) sitting inside a truncated octahedron with 24 vertices (Ag₂₄), both polyhedra with octahedral symmetry (Figure 3). The latter sits inside a rhombicosidodecahedron, an icosahedral polyhedral shell with 60 vertices (Ag₆₀), 20 triangles, 30 squares and 12 pentagons (Figure 2b).

Kepler’s Kosmos reappears
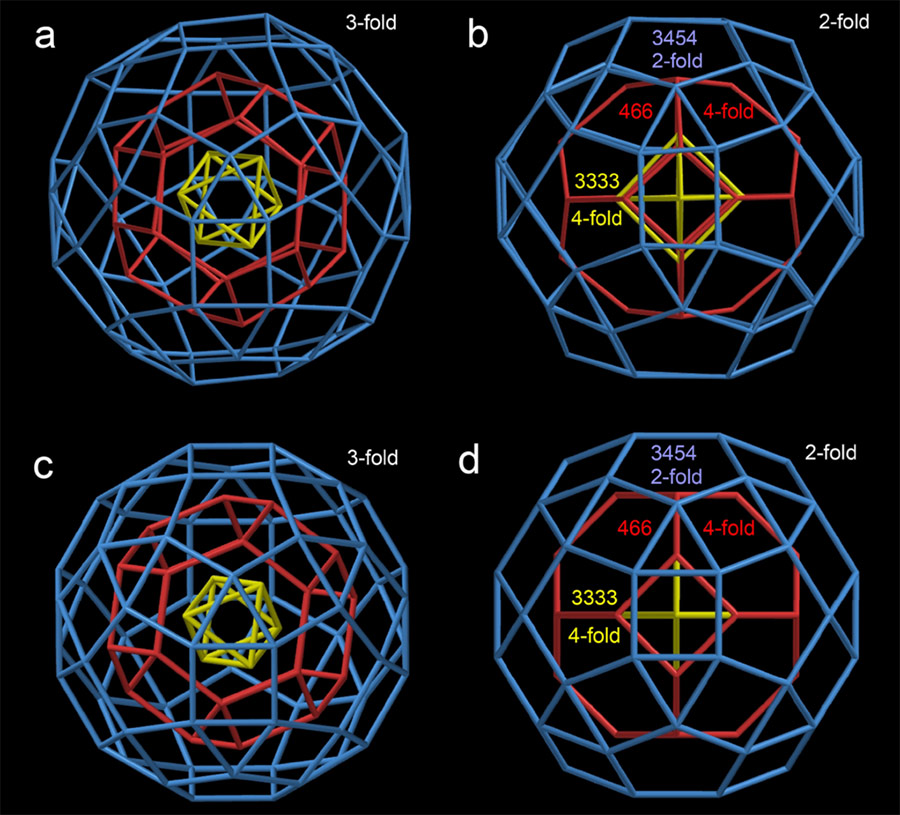
While an infinite number of alignments are possible, the newly synthesized Ag90 nanocluster possesses the most symmetric arrangement of two-/four- and three-fold axes of rotation (Figures 4a and 5). It also solves the seeming incompatibility of symmetry groups. Moreover, the alignment of this Keplerian nest is the same as in the Kepler’s Kosmos model devised by John Conway! In the words of Zometool’s Paul Hildebrandt, “Hats off to Sun, Schein, et al., who have bridged octahedral and icosahedral symmetry in the ‘real world’.”

In uniting these research streams, the investigators also explained the previously unrecorded merit of Conway’s model by showing that it maximizes the number of shared axes of rotational symmetry. Obviously, these solids could have been assembled without aligning the axes, just as Kepler himself had done. Moreover, they demonstrated that other, less optimal models could be constructed with fewer aligned axes of rotation (Figure 4b), thus highlighting the uniqueness of Conway’s arrangement.